Quantitative Reasoning
Key Terms
Stem: This is the information in which you are given, often in the form of a table, graph or chart. You will have to interpret this data using GCSE maths to answer questions.
Question: Each stem will have 4 questions attached to it, each with a choice of 5 options. There are some standalone stems which have only 1 question.
For Quantitive reasoning, you have to answer 36 questions in 25 minutes, giving you only 41 seconds per question. Most candidates agree that the timing for this section is the hardest aspect, so providing you have a strong GCSE maths knowledge, you should focus on time-saving tips. As most stems have 4 questions each, look out for the standalone stems. If you believe it will take you more than 40 seconds to interpret the information and calculate the answer of a standalone question: guess, flag and skip. These questions are often time-wasters and are there to slow down less experienced examinees. You can always come back at the end if you have time!
For this section, you will likely see questions which require:
Ability to calculate percentages, fractions and decimals, and convert between them.
Ability to calculate ratios and either: divide through by the smallest number to form a n : 1 ratio or by the highest common factor to simplify.
Manipulation of distance = speed x time and mass = density x volume equations.
Understanding of basic geometry.
Ability to work with numbers involving date and time.
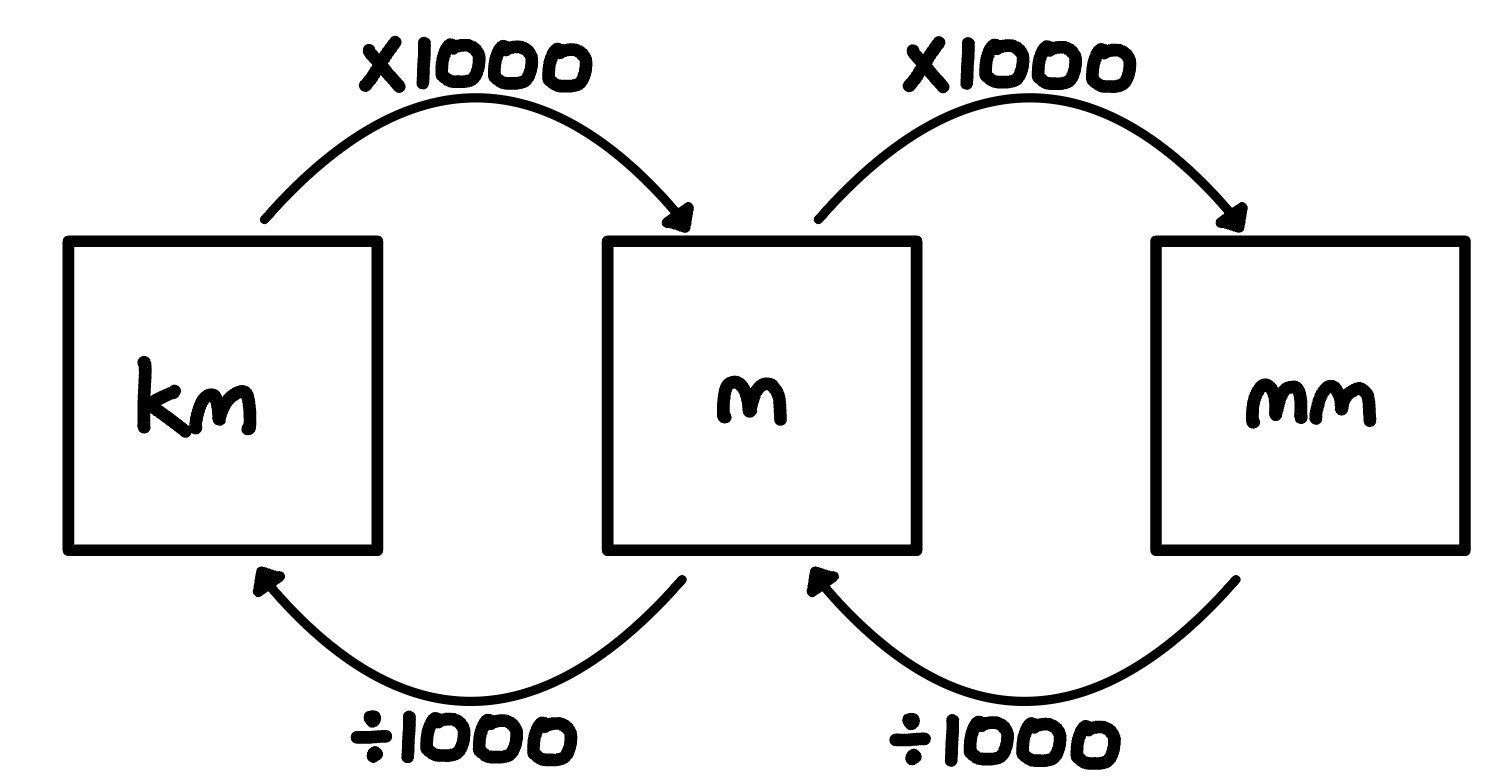
Ability to convert between units (kilometers per hour -> meters per second).
Ability to work with averages and calculate a mean.
In this guide, we have outlined what most people struggle with. Please note, the questions in the section below are to test your knowledge. Actual UCAT questions are always multiple choice, provide more information and often require multiple steps.
Percentages
You are almost guaranteed to come across a percentage change question in your UCAT test, therefore, ensure you are familiar with the equation. Do not be concerened if you get a negative number, this just indicates there is a percentage decrease.
1. Lana earned £1321 in 2021, and £1809 in 2022. Calculate the percentage increase in her earnings.
By simply plugging in the values into the equation, you can calculate the percentage change: 100 x (1809-1321)/1321 = 36.9%.
Ratios
A ratio compares values by showing how many there are of one thing compared to another (e.g. 12 : 8). A ratio, can be expressed in three forms:
Unsimplified: 12 : 8. This is a ratio which hasn’t been divided by the highest common factor (the largest number which divides into the two numbers of the ratio exactly).
Simplified: 3 : 2. This is the exact same as the previous ratio, however, it has been divided by the highest common factor of 12 and 8 (4) and thus is simplified.
A n : 1 ratio: 1.5 : 1. This is a ratio where you divide both numbers by the smallest number (in this case 8) so that one of the values is 1.
2. Lana earned £1321 in 2021, and £1809 in 2022. Express her earnings as a ratio of 1 : n.
Lana’s earnings, as a unsimplified ratio, are 1321 : 1809. You must divide through by the smallest number (1321) in order to express it as 1 : n. This will give you 1 : 1.37.
Converting Between Units
You may be less familiar with converting between different units. On the right, we have included two schematics to show you how to make single conversions between distances and time. The distance schematic is transferable to most other units (e.g ml and L).
When converting between a quantity which includes multiple units, you must use a multiplication factor which can be calculated with the equation shown. For example, if we are converting from km/h to m/s , you need to calculate the multiplication factor. The multiplier to convert from km -> m is x1000. The multiplier to convert between h -> s is 60 x 60 = x3600. Therefore, the multiplication factor is the top units/numerator (distance) divided by the bottom units/denominator (time), and thus to convert km/h -> m/s, multiply by 1000/3600.
3. Convert 53 km/h to m/s.
53km/h x 1000/3600 (as explained above) = 14.7 m/s
Interpreting Information
In order to improve your data interpretation, just do practice questions! As there are so many possible tables, graphs and charts, the best way to understand them, is to practice them. The more you do, the more familiar you will be. Ideally, if you complete enough past paper questions, you will not be surprised by any maths question that came up in the actual exam.
Time Saving Tips
As mentioned above, time is the most challenging aspect of this section. Furthermore, you are not able to take a calculator in the exam but instead, have an onscreen calculator as shown. This can’t store answers long term and it is very time consuming to use. Our best tips to save time are:
Attempt the question in your head first: When reading the question, quickly glance at the answers. If they are very far apart, and you feel you could make a good 'guesstimate” then do so. This will save valuable time. Instead, if you feel you can answer the question with some quick jottings on the whiteboard, do this. Try and minimise your calculator usage, as this is the slowest method. Only when the answers are close together (e.g if the answers are written to 1 decimal place, this is a good sign you will need the calculator), or the maths is too hard to do mentally, should you use the calculator. If, for example, you need to calculate a mean of 5 numbers, add these mentally or on the whiteboard using the column method, and then enter the result in the calculator to divide by 5.
Don’t be afraid to guess, flag and skip. Even the best mathematicians should guess, flag and skip some questions. As this isn’t about the best mathematicians, it’s about the fastest. Don’t let the time gobblers steal your time; guess, flag, skip and come back. At The Top Medic, we would skip around 5 questions on the first run-through.
Familiarise yourself with the calculator. For all practice papers, always use an onscreen calculator. The faster you can get at using it, the better you will perform in the exam.
Use “num-lock” and the number pad. In the actual exam, this should be switched on (but there’s no harm in checking). When practising, use the numbers to the right of your keyboard, as this saves time when typing numbers in.
When reading the stem, make a conscious effort to note the important facts and ignore the extra detail. Sometimes a key piece of information is hidden in the sentence before the graph or chart, other times this is flooded with extra unnecessary information. Acknowledge important information so that you know to return to it in later questions on the same stem.
Exam Style Question I
The table shows the total tax paid on an individual’s annual taxable income in dollars ($).
For example a person with an annual taxable income of 30,000$ will pay 4200$ plus 30% of 30,000-29,000$ (30% of 1,000$ = 300$). Therefore, 4,500$ in tax each year.
1. John has an annual taxable income of 18,250$. How much tax must he pay each year to the nearest dollar?
A. 1750$
D. 2300$
B. 2050$
E. 2475$
C. 2175$
2. Claire earns an annual taxable income of 675$ a week. She wants to save enough money so that she can pay off her tax at the end of the year. How much must she save, to the nearest dollar, each week?
A. 94$
D. 116$
B. 103$
E. 185$
C. 109$
3. Next year, the tax rate of each tax bracket is going to increase by 2.5% (i.e the lowest tax rate will be raised from 10% to 12.5%, the second tax rate will be raised from 20% to 22.5% etc.). By what percentage does the total tax paid increase for an individual who earns 30,000$?
A. 12.3%
D. 21.8%
B. 16.7%
E. 24.4%
C. 19.2%
Exam Style Question II
The incomplete table below shows the voting patterns in a constituency in 2016 and 2020.
1. Calculate the number of new young voters who became eligible or people who moved into the constituency between 2016 and 2020.
A. 2240
D. 8296
B. 2262
E. 8345
C. 8214
2. Provided there are only 4 parties up for election in 2016 and 2020, calculate the percentage increase in the (absolute) number of votes for the Blue Party.
A. 40%
D. 46%
B. 42%
E. 48%
C. 44%
3. Calculate the votes for Green Party expressed as a ratio of 2016:2020.
A. 1 : 1.13
D. 1 : 2.69
B. 1 : 1.29
E. 1 : 3.47
C. 1 : 1.41
Answers
Exam Style Question I
1. John has an annual taxable income of 18,250$. How much tax must he pay each year to the nearest dollar?
B. 2050$
As explained in the example given in the question, you can calculate the tax that John must pay by determining which income bracket he is in, and then adding the ‘Total Tax Paid at the Top of this Taxable Income Bracket’ of the bracket below. Therefore, in John’s case, 18,250$ places him in the second income bracket and so he must pay 20% tax on his earnings above 16,000$ and 1,600$ for the other 16,000$ of his earnings. Thus, his tax is: 20% of (18,250-16,200) + 1,600 = 0.2 x 2,250 + 1,600 = 2050$
2. Claire earns an annual taxable income of 675$ a week. She wants to save enough money so that she can pay off her tax at the end of the year. How much must she save, to the nearest dollar, each week?
D. 116$
In order to determine the tax Claire must pay, you need to determine her annual income. This is given by her weekly income x weeks in a year (52). Therefore, Claire’s annual income is 675$ x 52 = 35100$. You must then calculate the tax Claire needs to pay; she falls in the third tax bracket, so all her earnings over 29,000$ will be taxed at 30% and she will have to pay 4,200$ tax for the other 29,000$. Her yearly tax is: 0.3 x (35,100-29,000) + 4,200 = 6,030$. To calculate how much she must save per week, you must then divide this yearly figure by the number of weeks in a year (52). She must save 6030/52 = 116$ a week.
3. Next year, the tax rate of each tax bracket is going to increase by 2.5% (i.e the lowest tax rate will be raised from 10% to 12.5%, the second tax rate will be raised from 20% to 22.5% etc.). By what percentage does the total tax paid increase for an individual who earns 30,000$.
B. 16.7%
We can no longer used the total tax paid at the top of the income tax bracket as the tax rate has changed, so we must calculate the tax rate separately. For 30,000$, this means 16,000$ will be taxed at 12.5%, 29,000-16,000$ will be taxed at 22.5%, and 30,000-29,000$ will be taxed at 32.5%. The total tax paid under the new scheme is given by: 16,000 x 0.125 + 13,000 x 0.225 + 1,000 x 0.325 = 5250$. The example in the question gives us the usual tax paid on 30,000$ which is 4,500$; the percentage increase is given by 100 x (5250-4500)/4500 = 16.7%.
Exam Style Question II
1. Calculate the number of new young voters who became eligible or people who moved into the constituency between 2016 and 2020.
C. 8214
This question involves no complex maths, but tests your ability to understand the data given. We can see the first three rows link to the size of the electorate. To determine the number of new young voters who became eligible or voters who moved into the constituency, we need to calculate: the increase in size of electorate + number of voters who died or moved outside the constituency (we add these figures, because for the electorate to increase, we need to replace these dead/emigrators first). Therefore, the number of new young voters/voters who moved into the constituency is given by: 34,240-29,013 + 2,987 = 8,214.
2. Provided there are only 4 parties up for election in 2016 and 2020, calculate the percentage increase in the (absolute) number of votes for the Blue Party.
B. 42%
Firstly, you need to calculate the turnout in 2020 so that you can calculate the number of votes for the Blue Party. Then, you can then determine the percentage increase between these two numbers. To calculate the turnout, we know that 85% of the electorate voted, and so turnout equals 85% of 34,240 (0.85 x 34,240) = 29,104. To calculate the votes for Blue Party, you need to subtract the votes given to the other parties from the total number of votes (29,104-3,451-8,541-2,017) = 15,095. Finally, to calculate absolute percentage increase from 2016 to 2020: 100 x (15,095-10,634)/10,634 = 42%.
‘Absolute’ simply means the actual numbers (10,634 and 15,095) rather than, for example, calculating the percentage increase in the proportion of voters who chose Blue Party.
3. Calculate the votes for Green Party expressed as a ratio of 2016:2020.
A. 1 : 1.13
This question requires you to calculate a ratio. Firstly, you must determine the number of votes for Green Party in 2016 by subtracting the number of votes for the other parties from the total number of votes. Then, to calculate the 1 : n ratio, divide both of the numbers by the smaller number. The number of votes for Green Party in 2016 is 23,099-1,283-3,638-10,634) = 7,544. The ratio is thus 7,544 : 8,514. Dividing both sides by the smallest number (7,544) will give you 1 : 1.13.